Laboratorio 6
ESERCIZIO XVI
Funzioni ricorsive
- Scrivere un programma che calcoli il fattoriale di un numero dato in input dall’utente. Il programma dovra fare uso di funzioni ricorsive.
- Scrivere una funzione ricorsiva che calcoli la somma degli elementi di un vettore dato in ingresso.
Soluzione
# Punto 1
def fattoriale(n):
if n == 1 or n == 0:
return 1
return n * fattoriale(n-1)
num = int(raw_input("scegli un numero di cui calcolare il fattoriale:"))
print fattoriale(num)
# Punto 2
def somma(vect):
if len(vect) == 1:
return vect[0]
return vect[0] + somma(vect[1:])
ESERCIZIO XVII
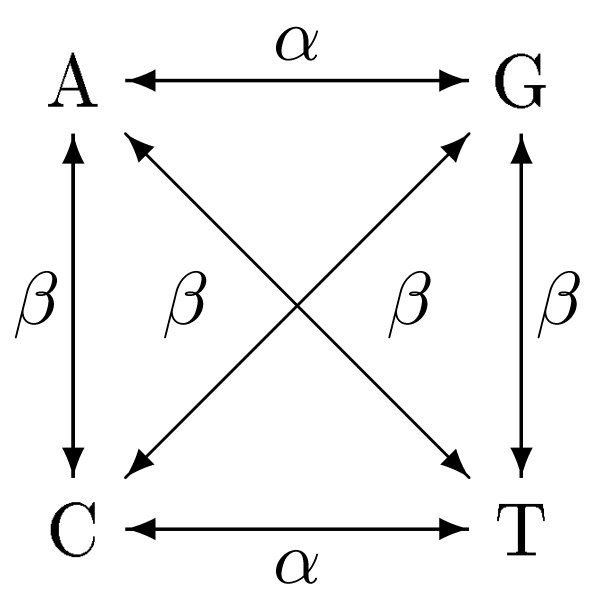
Si consideri un modello di evoluzione della sequenza del DNA basato su catene di Markov. Si faccia riferimento al modello definito da Jukes e Cantor, come mostrato in figura (si ricordi che per JK ). Wikipedia, Libro.
Codice fornito MarkovChain.py.
Alcuni esempi:
>>> nuc_mc = JC69('A')
<__main__.MarkovChain instance at 0x1a22066638>
...
>>> nuc_mc.get_state()
'A'
>>> nuc_mc.move()
'True'
>>> nuc_mc.get_state()
'C'
Utilizzado il codice fornito si:
-
Generi una sequenza casuale di lunghezza 100 nucleotidi; si generi un modello di Jukes e Cantor per ogni nucleotide, e si faccia evolvere la sequenza per 100 passi. Si stampi a video la distanza di hamming tra la sequenza originale e la sequenza evoluta.
- Generi una sequenza casuale di lunghezza 100 nucleotidi; si generi un modello di Jukes e Cantor per ogni nucleotide, e si faccia evolvere la sequenza per 100 mutazioni. Si stampi a video la distanza di hamming tra la sequenza originale e la sequenza evoluta.
-
Ripetendo l’esperimento definito al punto 2 per un certo numero k (es: k=10) volte, si stimi distanza di hamming media tra la sequenza originale e la sequenze evolute. Questo rappresenta un punto sul grafico in figura, dove k rappresenta il numero di mutazioni e c la distanza misurata.
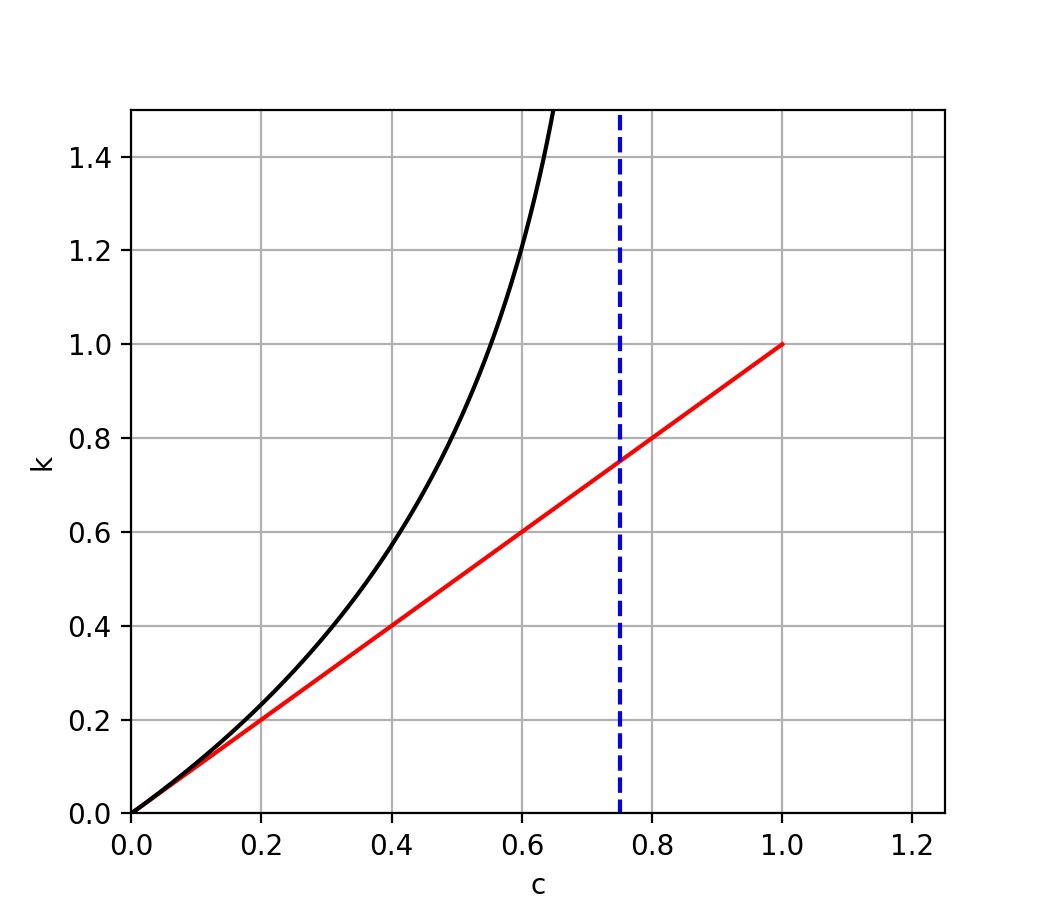
- Ripetendo l’esperimento del punto 3 per diversi valori del numero di mutazioni, si stimi l’intero grafico.
Soluzione
import random
from MarkovChain import JC69
import numpy as np
def hdist(s,t):
d = sum(ch1!=ch2 for ch1,ch2 in zip(s,t))
return d
length = 100
seq0= "".join([random.choice("ACGT") for x in range(length)])
print "initial sequence:\n"+seq0
print
#%%
# Punto I
num_steps = 100
models = [JC69(nuc) for nuc in seq0]
for i in xrange(num_steps):
for model in models:
model.move()
seq1 = ''.join(model.get_state() for model in models)
print "Hamming distance after %d steps:" % \
(num_steps), hdist(seq0,seq1)
print
#%%
# Punto II
num_mutations = 100
models = [JC69(nuc) for nuc in seq0]
access_sequence = range(length)
random.shuffle(access_sequence) #all models accessed in random sequence
count_mutations = 0
while count_mutations < num_mutations:
for i in access_sequence: #all models accessed in random sequence
evolved = models[i].move() # remember: True -> 1, False -> 0
count_mutations += evolved
if count_mutations == num_mutations:
break
seq2 = ''.join(model.get_state() for model in models)
print "Hamming distance after %d mutations: %s" % \
(num_mutations , hdist(seq0,seq2) )
print
#%%
# Punto III
num_tests = 10
num_mutations = 100
results_list = [] #list to host test results
for k in xrange(num_tests):
models = [JC69(nuc) for nuc in seq0]
access_sequence = range(length)
random.shuffle(access_sequence) #all models accessed in random sequence
count_mutations = 0
while count_mutations <num_mutations:
for i in access_sequence: #all models accessed in random sequence
evolved = models[i].move()
count_mutations += evolved
if count_mutations == num_mutations:
break
seq3 = ''.join(model.get_state() for model in models)
results_list.append(hdist(seq0,seq3))
print "Avg Hamming distance after %d mutations in %d tests: %.2f +- %.2f" % \
(num_mutations, num_tests, np.mean(results_list), np.std(results_list) )
print
#%%
# Punto IV
num_tests = 1
#num_mutations = int(length*3.1)
num_mutations = 100
#numpy array to host test results
total_arr = np.zeros((num_tests,num_mutations))
for k in xrange(num_tests):
print "Test n.: %d for %d mutations" % (k+1,num_mutations)
models = [JC69(nuc) for nuc in seq0]
count_mutations = 0
access_sequence = range(length)
random.shuffle(access_sequence) #all models accessed in random sequence
while count_mutations < num_mutations:
for i in access_sequence:
evolved = models[i].move()
count_mutations += evolved
if count_mutations == num_mutations:
break
if evolved:
seq4 = ''.join(model.get_state() for model in models)
total_arr[k,count_mutations] = hdist(seq0, seq4)
from MarkovChain import plot_gen
plot_gen(total_arr, length)
ESERCIZIO XVIII
Scrivere un programma che:
-
Dati due vettori, crei la matrice del prodotto . Ideare una struttura dati appropriata per implementare la matrice.
- Completare il programma con una stampa della matrice riga per riga:
[6, 7, 8 ... ]
[12 , 14, 16 ... ]
... - Aggiungere una funzione stampa_matrice(mat), che migliori la stampa:
stampa_matrice(mat)
6 7 8 9 10
12 14 16 18 20
18 21 24 27 30
...
Per fare in modo che i numeri siano stampati allineati, usare per ogni numero il costrutto di string formatting come riportato:
print '%3i' % num
Soluzione
import numpy as np
vector_1 = np.array([1,2,3,4,5])
vector_2 = np.array([6,7,8,9,10])
matrix = []
for elem in vector_1:
row = elem*vector_2
matrix.append(row)
for row in np.array(matrix):
print row
print
# Soluzione list comprehension
matrix = [elem*vector_2 for elem in vector_1]
print np.array(matrix)
print
# Punto II
def stampa_matrice(matrix):
for row in matrix :
for num in row :
print '%3i' % num,
print
print
stampa_matrice(matrix)